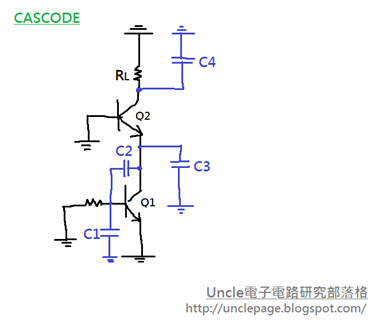
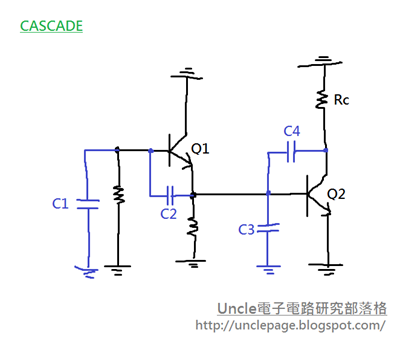
最近讀到薛丁格方程式(Schrodinger Equation),讓我回憶起高中學的近代物理,現在對當年讀的內容有更深的了解。
一個維度的薛丁格方程式如下:
我對於這個式子的基本理解
這個式子的推導,是由動能+位能守恆的觀念得來的。描述的是量子世界中,粒子具有波動性,就是說在微小的量子世界中,看到的粒子已經是一種波動的狀態(可以用波動方程式描述),無法確定這個粒子的特定位置,但能描述粒子出現在特定位置的機率。
上面提到粒子的波動,就可以用來描述,
就是波函數,
就是機率密度函數(CDF)。
討論一下是什麼:
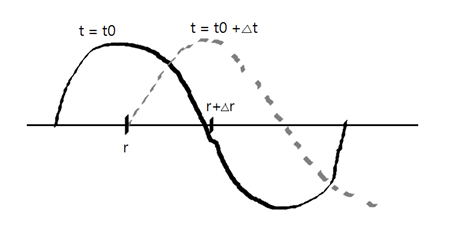
對照我之前讀過的電磁學,這是一個波函數的標準形式,類似訊息載在載波上傳遞出去。也因此可以推導期相速和群速。現在,考慮一個波在極短的時間內,移動了:
所以peak的位置函數值應該相同:
古典與近代物理的能量、動量、速度表示法
很多時候,我們比較感興趣的是粒子的動能E跟動量p。
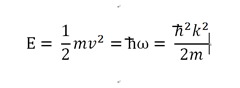
上面的式子裡,h上面多一個bar,代表是planck constant除以的意思。所以可以仔細的理解到,如果已知頻率,就可以很容易地利用h-bar來描述這個粒子的動能。至於動量:
可以了解到,得知k,就可以很容易地利用h-bar得到粒子的動量。接這討論速度:
有趣的地方是相速只是古典物理中速度的一半而已。
這就是這學期我開始學到薛丁格方式的基礎,以後若有更多的心得會再補上來。

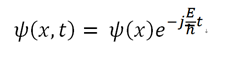
![clip_image002[23] clip_image002[23]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhLHQKgA2ok-CStcCQowuhAKXGSjQUS8R_l25Vc98_Gv0GQETHak-WhCgMCOiKCwmuDXaVo7fFUeRE_WJ1lzoSSdRLLiWKlPFrFikS_gH1jJZpyydj8SyhU4AYEpbGNQKSzT4DiyLoewgHo/?imgmax=800)
![clip_image002[27] clip_image002[27]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjRgifHbwxWFb8uuAoBoedKhKcw6m4fWUoTvadbj2sVhSY0Vu4GK5cQ9Nth9-yEDM8hcqvSJfPLfsndhVmDKIzOM-sg4wIWBB87PQrhI1v3U9dY4NNbV4dS4_2kLD4zEyrO-aV4gudj7a5h/?imgmax=800)

![clip_image002[31] clip_image002[31]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiryu7uZJxnvVxzgwuC34OGsfnJfHNK6Ni62OoFzU6lhuzO6TshjiROAvp3NoyAPOjv76e7CLfs29QDmqhIFIZNWqr1MjNuNN-JmgNx3j4QS2NuWt-rzFTKXHvEBRXhI5l0ZqnUY96aZ2dD/?imgmax=800)



![clip_image002[22] clip_image002[22]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhaoZ4RFFxZitS6RpYNtArjP8fHPOmnacEUSpA0IKlZSzItfOKG971IicgEtNaa85QrIS697SrBKmzZBkp7PBH0glw0ru7yoy3hBE7v3yEUh2Jz_ZV8-I6pTXxo4F_uxDT0OmdhuzvUe7VB/?imgmax=800)



![clip_image002[9] clip_image002[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgUX15vHzZR9rF6rdZzw128iyLxA1LXnigKNV8vPuloxgsLtqgRVsNWariVIwt7dKoCOj_mfISrko8UToWa2qDdffVn4ob26aU6d9rPBpCkOCR8aUyzRfZCHCxM5FxIWa2y7Y8rj8mb07sh/?imgmax=800)